Mit dem oben konstruierten Graphen einschließlich Bewertung wird nun der kostenminimale Fluss bestimmt. Die Parameter für die Zielkostenfunktion können Sie dabei einstellen, wie bereits im vorherigen Verfahrensschritt beschrieben. So können Sie also insbesondere die Ausgestaltung des in der Einleitung beschriebenen Zielkonflikts zwischen Minimierung der Leerfahrten und Minimierung des Fahrzeugbedarfs steuern. Abbildung 201 zeigt schematisch einen solchen kostenminimalen Fluss, wobei mehrere Flusseinheiten (Fahrzeugkombinationen) auf einer Kante durch übereinander gestapelte Linien angedeutet sind. Aus Gründen der Vereinfachung sind hier keine Kosten und Kapazitäten vermerkt. Sie können der Abbildung aber entnehmen, dass alle Fahrplanfahrtabschnitte genau von einer Fahrzeugkombination befahren werden. Sie können dem Graphen außerdem entnehmen, welche Leerfahrten im kostenminimalen Fluss überhaupt gefahren werden müssen (nämlich alle vom Fluss überquerten Kanten). Insgesamt sind es zwei Leerfahrten – eine von C´ nach A und eine von B nach C´. Die Bewertungslinie schneidet drei Kanten, weswegen der Fahrzeugbedarf 3 beträgt.
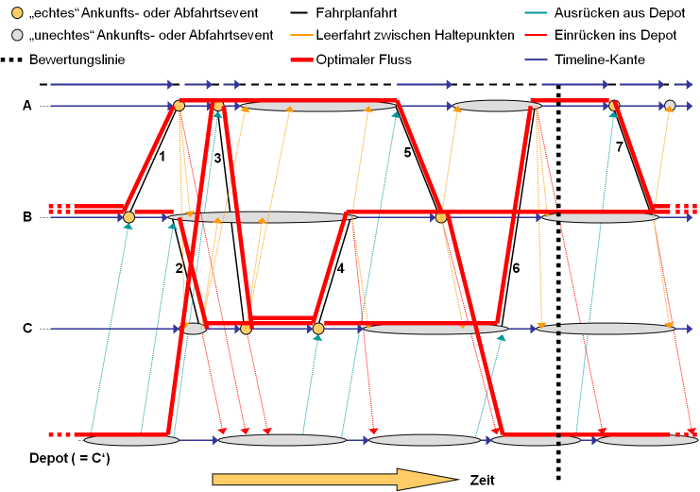
Abbildung 201: Kostenoptimaler Fluss im Beispielgraph
Als Ergebnis dieses Schrittes liegt also ein kostenminimaler Fluss vor, und man kennt den Fahrzeugbedarf und weiß, welches die notwendigen Leerfahrten sind. Noch nicht bekannt sind hingegen die Umläufe selbst, also an welchen Haltepunkten Umläufe beginnen und enden und welchen Weg sie im optimalen Fluss nehmen.

